二叉查找树是常用的一种二叉树，他支持快速插入，删除，查找操作，各个操作的时间复杂度跟树的高度成正比，理想情况下，时间复杂度是O(logn)

1. 二叉树中任意一个节点的左右子树的高度相差不能大于1。所以完全二叉树，满二叉树都是平衡二叉树，非完全二叉树也有可能是平衡二叉树。
2. 平衡二叉查找树不仅满足上面平衡二叉树的定义，还满足二叉查找树的特点。
3. 发明平衡二叉查找树这类数据结构的初衷是解决普通二叉查找树在频繁的插入，删除等动态更新的情况下，出现时间复杂度退化的问题。所以，平衡二叉查找树中“平衡”的意思，其实就是让整棵树左右看起来比较“对称”，比较“平衡”，不要出现左子树很高，右子树很矮的情况。这样就能让整颗树的高度相对低一些，相应的插入，删除，查找等操作的效率高一些。
4. 若设计一个新的平衡二叉查找树，只要树的高度不比log2n大很多（如树的高度仍然是对数量级的），尽管它不符合严格的平衡二叉查找树的定义，但它仍然可以被认为是一个合格的平衡二叉查找树。

理解红黑树之前，必须先了解另一种树，叫2-3树，红黑树背后的逻辑就是它

1. 2-3树是二叉查找树的变种，树中的2和3代表两种节点，以下表示为2-节点和3-节点。
2. 2-节点即普通节点：包含一个元素，两条子链接。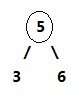
   
3. 3-节点则是扩充版，包含2个元素和三条链接：两个元素A、B，左边的链接指向小于A的节点，中间的链接指向介于A、B值之间的节点，右边的链接指向大于B的节点。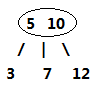

4. 一颗完美平衡的2-3查找树中的所有空链接到根结点的距离都是相同的。

要判断一个键是否在树中，我们先将它和根结点中的键比较。如果它和其中的任何一个相等，查找命中。否则我们就根据比较的结果找到指向相应区间的链接，并在其指向的子树中递归地继续查找。如果这是个空链接，查找未命中。

1. 要在2-3树中插入一个新结点，我们可以和二叉查找树一样先进行一次未命中的查找，然后把新结点挂在树的底部。但这样的话树无法保持完美平衡性。我们使用2-3树的主要原因就在于它能够在插入之后继续保持平衡。

2. 如果未命中的查找结束于一个2-节点，我们只要把这个2-节点替换为一个3-节点，将要插入的键保存在其中即可。如果未命中的查找结束于一个3-结点，事情就要麻烦一些.

   1. 情况一：只有一个3-结点的树，向其插入一个新键
      将3-节点扩充为一个4-节点，即包含三个元素的节点，然后将其分解，变成一棵二叉树

      

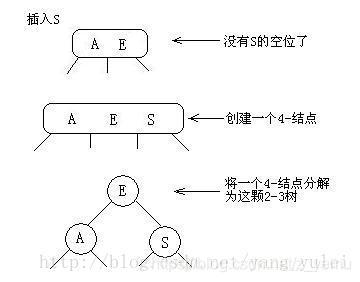
   2. 情况二：向一个父节点为2-节点的3-节点中插入新键

      此时一样将 3-节点扩充为4-节点，但不为中键创建一个新的节点，而是分解4-节点，将中键移动到父节点

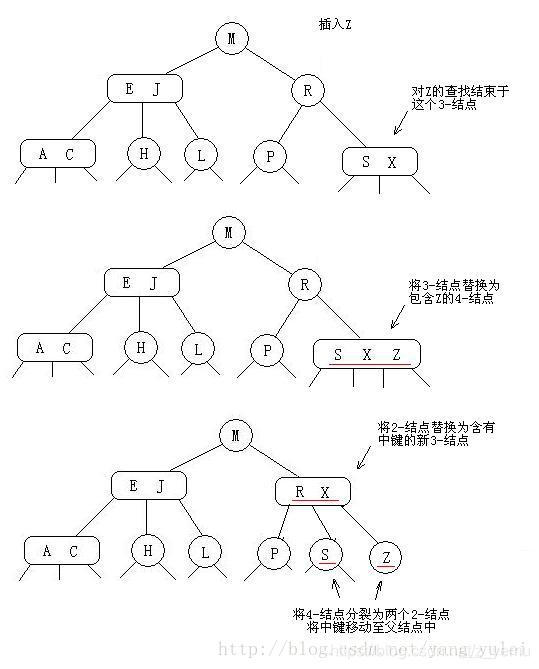
3. 情况三：向一个父节点为3-节点的3-节点中插入新键
   和刚才一样构造一个临时的4-节点并分解它，然后将它的中键插入它的父节点中。但父节点也是一个3-节点，因此再用这个中键构造一个新的临时4-节点，然后在这个节点上进行相同的变换，即分解这个父结点并将它的中键插入到它的父结点中去。就这样，一直向上不断分解临时的4-节点并将中键插入更高的父节点，直至遇到一个2-节点，然后根据情况二处理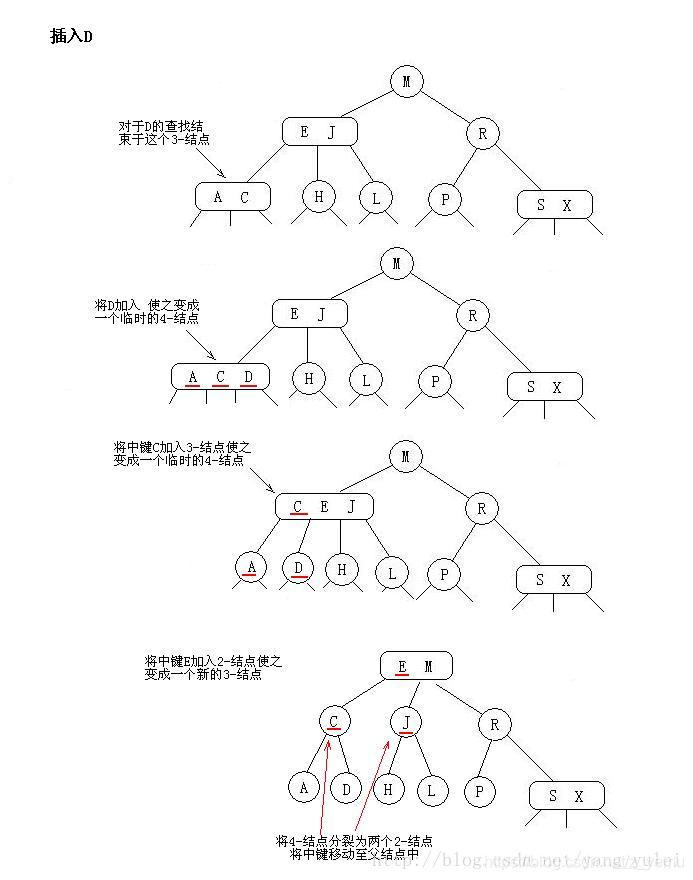

当你了解了这些后，便可以看红黑树。

1. 红黑树：英文“Red-Black-Tree”，简称R-B Tree，有如下特性：
   1. 根节点是黑色的；
   2. 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；
   3. 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
   4. 每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点
2. 红黑树的高度分析
   1. 首先，将红色节点从红黑树中去除，那单纯包含黑色节点的红黑树的高度比包含相同节点个数的完全二叉树的高度要小。所以去掉红色节点的“黑树”的高度也不会超过log2n。
   2. 在红黑树中，红色节点不能相邻，即有一个红色节点就要至少有一个黑色节点，将它更其他红色节点隔开。红黑树中包含最多黑色节点的路径不会超过log2n, 所以加入红色节点之后，最长路径不会超过 2log2n，即，红黑树的高度近似2log2n
   3. 红黑树的高度只比高度平衡的AVL树的高度（log2n）仅仅大了一倍，在性能上下降的并不多。

上面这些没看懂也没关系，通俗易懂话来讲：红黑树就是用红链接表示 3-节点的 2-3树

红黑树中，所有的节点都是标准的2-节点，为了体现出3-节点，这里将3-节点的两个元素用左斜红色的链接连接起来，即连接了两个2-节点来表示一个3-节点。这里红色节点标记就代表指向其的链接是红链接，黑色标记的节点就是普通的节点。固有红黑树的另一种定义是满足下列条件的二叉查找树：

1. 红链接均为左链接。

2. 没有任何一个结点同时和两条红链接相连。(这样会出现4-节点)

3. 该树是完美黑色平衡的，即任意空链接到根结点的路径上的黑链接数量相同。

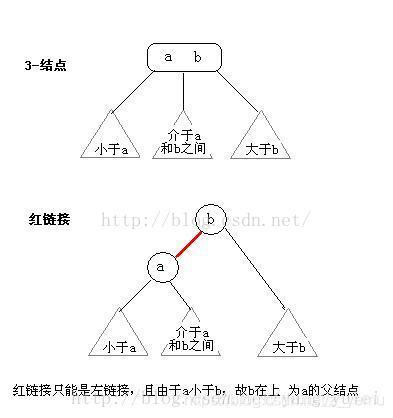
这里其实就是将 3-节点 中的两个元素用二叉树形式表现出来

①：Treap，Splay Tree，绝大部分情况下，它们操作的效率都很高，但是也无法避免极端情况下时间复杂度的退化。尽管这种情况出现概率不大，但是对于单次操作时间非常敏感的场景来讲，它们不适用。
②：AVL树是一种高度平衡的二叉树，所以查找的效率非常高，但是，有利有弊，AVL树为了维持这种高度平衡，要付出更多代价，每次插入，删除都要做调整，就比较复杂，耗时。所以有频繁的插入，删除操作的数据集合，使用AVL树的代价就有点高了。
③：红黑树只是做到了近似平衡，并不是严格的平衡，所以维护平衡的成本上，要比AVL树低。
所以，红黑树的插入，删除，查找各种操作性能都比较稳定。对于工程应用来说，结果状态可控可预期。