决策树

决策树是个超简单结构，我们每天都在头脑中使用它。它代表了我们如何做出决策的表现形式之一，他是一系列if–then-else规则的集合

先看一个决策树的例子，决定某人是否应该在特定的一天打棒球。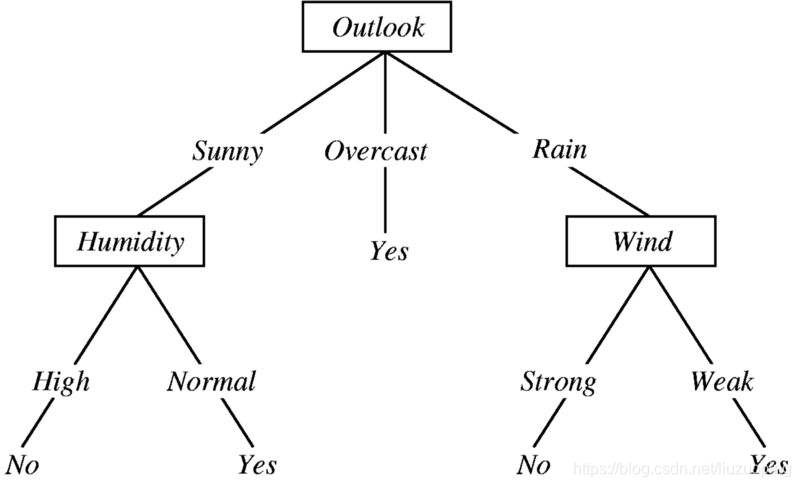
决策树具备以下特性：

1、决策树用于建模非线性关系（与线性回归模型和逻辑回归模型相反）
2、决策树可以对分类和连续结果变量进行建模，尽管它们主要用于分类任务（即分类结果变量）
3、决策树很容易理解！ 您可以轻松地对它们进行可视化，并准确找出每个分割点发生的情况。 您还可以查看哪些功能最重要
4、决策树容易过拟合。这是因为无论通过单个决策树运行数据多少次，因为只是一系列if-then-else语句，所以总是会得到完全相同的结果。这意味着决策树可以非常精确地适配训练数据，但一旦开始传递新数据，它可能无法提供有用的预测

决策树有多种算法，最常用的是ID3（ID代表“迭代二分法”）和CART（CART代表“分类和回归树”）。这些算法中的每一个都使用不同的度量来决定何时分割。ID3树使用信息增益 ，而CART树使用基尼指数 。

三大经典决策树算法最主要的区别在于其特征选择准则的不同。ID3算法选择特征的依据是信息增益、C4.5是信息增益比，而CART则是Gini指数。作为一种基础的分类和回归方法，决策树可以有如下两种理解方式。一种是我们可以将决策树看作是一组if-then规则的集合，另一种则是给定特征条件下类的条件概率分布。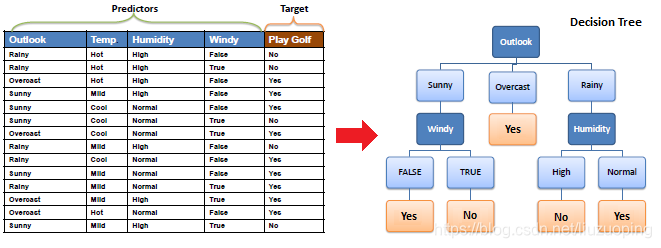

在讲信息增益之前，这里我们必须先介绍下熵的概念。在信息论里面，熵是一种表示随机变量不确定性的度量方式。若离散随机变量X的概率分布为：

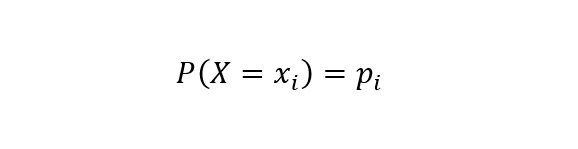则随机变量X的熵定义为：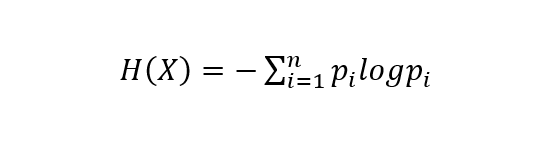

同理，对于连续型随机变量Y，其熵可定义为：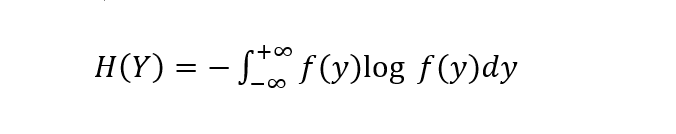
当给定随机变量X的条件下随机变量Y的熵可定义为条件熵H(Y|X)：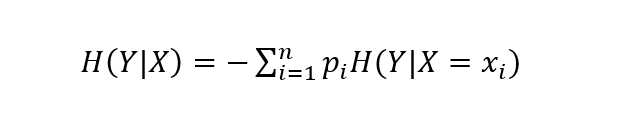

若数据集D的信息熵为H(D)，给定特征A之后的条件熵为H(D|A)，则特征A对于数据集的信息增益g(D,A)可表示为：

g(D,A) = H(D) - H(D|A)

def entropy(ele):    
    # Calculating the probability distribution of list value
    probs = [ele.count(i)/len(ele) for i in set(ele)]    
    # Calculating entropy value
    entropy = -sum([prob*log(prob, 2) for prob in probs])    
    return entropy

def split_dataframe(data, col):    
    # unique value of column
    unique_values = data[col].unique()    
    # empty dict of dataframe
    result_dict = {elem : pd.DataFrame for elem in unique_values}    
    # split dataframe based on column value
    for key in result_dict.keys():
        result_dict[key] = data[:][data[col] == key]    
    return result_dict

def choose_best_col(df, label):    
    # Calculating label's entropy
    entropy_D = entropy(df[label].tolist())    
    # columns list except label
    cols = [col for col in df.columns if col not in [label]]    
    # initialize the max infomation gain, best column and best splited dict
    max_value, best_col = -999, None
    max_splited = None
    # split data based on different column
    for col in cols:
        splited_set = split_dataframe(df, col)
        entropy_DA = 0
        for subset_col, subset in splited_set.items():            
            # calculating splited dataframe label's entropy
            entropy_Di = entropy(subset[label].tolist())            
            # calculating entropy of current feature
            entropy_DA += len(subset)/len(df) * entropy_Di        
        # calculating infomation gain of current feature
        info_gain = entropy_D - entropy_DA        
        if info_gain > max_value:
            max_value, best_col = info_gain, col
            max_splited = splited_set    
        return max_value, best_col, max_splited

class ID3Tree:    
    # define a Node class
    class Node:        
        def __init__(self, name):
            self.name = name
            self.connections = {}    
            
        def connect(self, label, node):
            self.connections[label] = node    
        
    def __init__(self, data, label):
        self.columns = data.columns
        self.data = data
        self.label = label
        self.root = self.Node("Root")    
    
    # print tree method
    def print_tree(self, node, tabs):
        print(tabs + node.name)        
        for connection, child_node in node.connections.items():
            print(tabs + "t" + "(" + connection + ")")
            self.print_tree(child_node, tabs + "tt")    
    
    def construct_tree(self):
        self.construct(self.root, "", self.data, self.columns)    
    
    # construct tree
    def construct(self, parent_node, parent_connection_label, input_data, columns):
        max_value, best_col, max_splited = choose_best_col(input_data[columns], self.label)        
        if not best_col:
            node = self.Node(input_data[self.label].iloc[0])
            parent_node.connect(parent_connection_label, node)            
        return

        node = self.Node(best_col)
        parent_node.connect(parent_connection_label, node)

        new_columns = [col for col in columns if col != best_col]        
        # Recursively constructing decision trees
        for splited_value, splited_data in max_splited.items():
            self.construct(node, splited_value, splited_data, new_columns)

from sklearn.datasets import load_iris
from sklearn import tree
import graphviz

iris = load_iris()
# criterion选择entropy，这里表示选择ID3算法
clf = tree.DecisionTreeClassifier(criterion='entropy', splitter='best')
clf = clf.fit(iris.data, iris.target)

dot_data = tree.export_graphviz(clf, out_file=None,
                               feature_names=iris.feature_names,
                               class_names=iris.target_names,
                               filled=True, 
                               rounded=True,
                               special_characters=True)
graph = graphviz.Source(dot_data)
graph

所谓CART算法，全名叫Classification and Regression Tree，即分类与回归树。顾名思义，相较于此前的ID3算法和C4.5算法，CART除了可以用于分类任务外，还可以完成回归分析。完整的CART算法包括特征选择、决策树生成和决策树剪枝三个部分。

CART算法主要包括回归树和分类树两种。回归树用于目标变量为连续型的建模任务，其特征选择准则用的是平方误差最小准则。分类树用于目标变量为离散型的的建模任务，其特征选择准则用的是基尼指数(Gini Index)，这也有别于此前ID3的信息增益准则和C4.5的信息增益比准则。无论是回归树还是分类树，其算法核心都在于递归地选择最优特征构建决策树。

给定输入特征向量X和输出连续型变量Y，一个回归树的生成就对应着输入空间的一个划分以及在划分的单元上的输出值。假设输入空间被划分为M个单元R1，R2…，RM，在每一个单元Rm上都有一个固定的输出值Cm，所以回归树模型可以表示为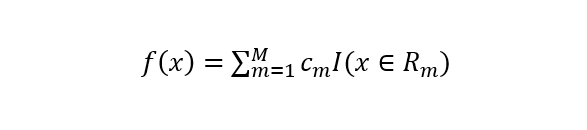
在输入空间划分确定时，回归树算法使用最小平方误差准则来选择最优特征和最优且切分点。具体来说就是对全部特征进行遍历，按照最小平方误差准则来求解最优切分变量和切分点。即求解如下公式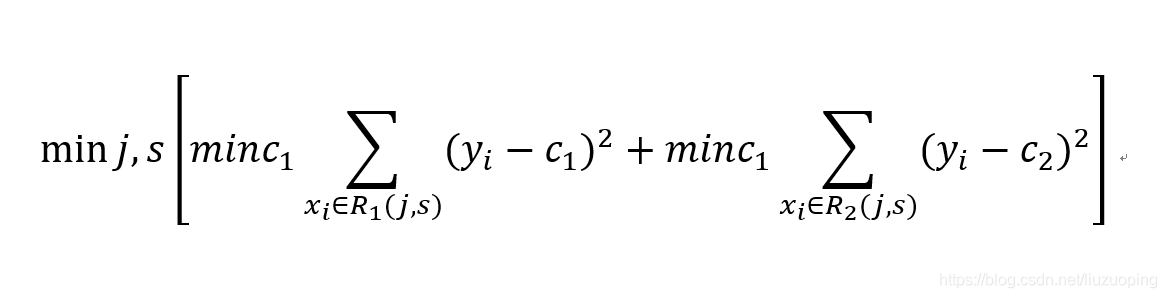

  CART分类树跟回归树大不相同，但与此前的ID3和C4.5基本套路相同。ID3和C4.5分别采用信息增益和信息增益比来选择最优特征，但CART分类树采用Gini指数来进行特征选择。先来看Gini指数的定义。

  Gini指数是针对概率分布而言的。假设在一个分类问题中有K个类，样本属于第k个类的概率为Pk，则该样本概率分布的基尼指数为

具体到实际的分类计算中，给定样本集合D的Gini指数计算如下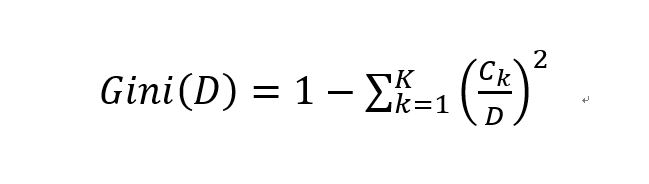
相应的条件Gini指数，也即给定特征A的条件下集合D的Gini指数计算如下
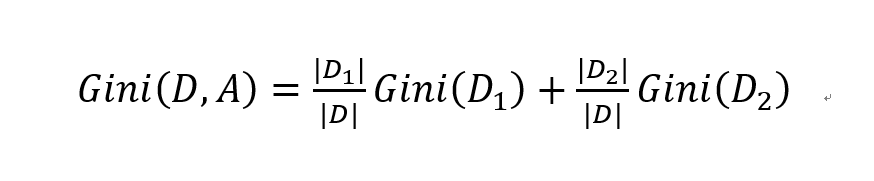完整的分类树构造算法如下：(来自统计学习方法)

所谓剪枝，就是将构造好的决策树进行简化的过程。具体而言就是从已生成的树上裁掉一些子树或者叶结点，并将其根结点或父结点作为新的叶结点。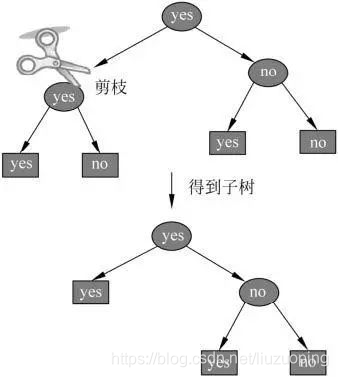
通常来说，有两种剪枝方法。一种是在决策树生成过程中进行剪枝，也叫预剪枝(pre-pruning)。另一种就是前面说的基于生成好的决策树自底向上的进行剪枝，又叫后剪枝(post-pruning)。

  先来看预剪枝。预剪枝是在树生成过程中进行剪枝的方法，其核心思想在树中结点进行扩展之前，先计算当前的特征划分能否带来决策树泛化性能的提升，如果不能的话则决策树不再进行生长。预剪枝比较直接，算法也简单，效率高，适合大规模问题计算，但预剪枝可能会有一种”早停”的风险，可能会导致模型欠拟合。

  后剪枝则是等树完全生长完毕之后再从最底端的叶子结点进行剪枝。CART剪枝正是一种后剪枝方法。简单来说，就是自底向上对完全树进行逐结点剪枝，每剪一次就形成一个子树，一直到根结点，这样就形成一个子树序列。然后在独立的验证集数据上对全部子树进行交叉验证，哪个子树误差最小，哪个就是最优子树。具体细节可参考统计学习方法给出的剪枝算法步骤，笔者这里不深入展开公式。

 class CartTree:    
    # define a Node class
    class Node:        
        def __init__(self, name):
            self.name = name
            self.connections = {}    

        def connect(self, label, node):
            self.connections[label] = node    

    def __init__(self, data, label):
        self.columns = data.columns
        self.data = data
        self.label = label
        self.root = self.Node("Root")    

    # print tree method
    def print_tree(self, node, tabs):
        print(tabs + node.name)        
        for connection, child_node in node.connections.items():
            print(tabs + "t" + "(" + connection + ")")
            self.print_tree(child_node, tabs + "tt")    

    def construct_tree(self):
        self.construct(self.root, "", self.data, self.columns)    

    # construct tree
    def construct(self, parent_node, parent_connection_label, input_data, columns):
        min_value, best_col, min_splited = choose_best_col(input_data[columns], self.label)   
        if not best_col:
            node = self.Node(input_data[self.label].iloc[0])
            parent_node.connect(parent_connection_label, node)            
            return

        node = self.Node(best_col)
        parent_node.connect(parent_connection_label, node)

        new_columns = [col for col in columns if col != best_col]        
        # Recursively constructing decision trees
        for splited_value, splited_data in min_splited.items():
            self.construct(node, splited_value, splited_data, new_columns)

又涨姿势了吧~