社区微信群开通啦,扫一扫抢先加入社区官方微信群

社区微信群
社区微信群开通啦,扫一扫抢先加入社区官方微信群

社区微信群
英文原文链接:http://theory.stanford.edu/~amitp/GameProgramming/
英文原文参考:http://www-cs-students.stanford.edu/%7Eamitp/gameprog.html#Paths
翻译参考链接:http://blog.csdn.net/b2b160/article/details/4057781
我们尝试解决的问题是把一个游戏对象(game object)从出发点移动到目的地。路径搜索(Pathfinding)的目标是找到一条好的路径——避免障碍物、敌人,并把代价(燃料,时间,距离,装备,金钱等)最小化。运动(Movement)的目标是找到一条路径并且沿着它行进。把关注的焦点仅集中于其中的一种方法是可能的。一种极端情况是,当游戏对象开始移动时,一个老练的路径搜索器(pathfinder)外加一个琐细的运动算法(movement algorithm)可以找到一条路径,游戏对象将会沿着该路径移动而忽略其它的一切。另一种极端情况是,一个单纯的运动系统(movement-only system)将不会搜索一条路径(最初的“路径”将被一条直线取代),取而代之的是在每一个结点处仅采取一个步骤,同时考虑周围的环境。同时使用路径搜索(Pathfinding)和运动算法(movement algorithm)将会得到最好的效果。
移动一个简单的物体(object)看起来是容易的。而路径搜索是复杂的。为什么涉及到路径搜索就产生麻烦了?考虑以下情况:
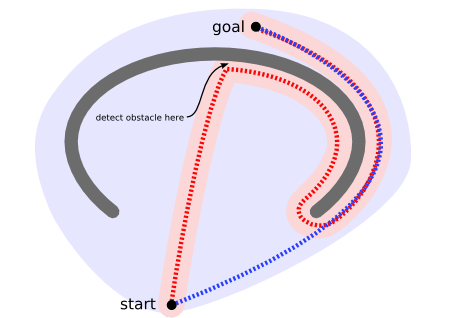
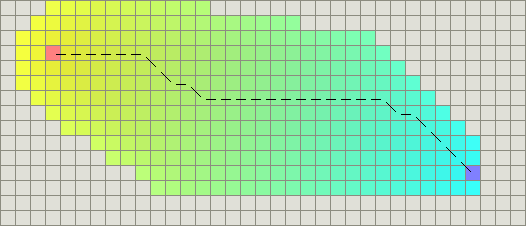
物体(unit)最初位于地图的底端并且尝试向顶部移动。物体扫描的区域中(粉红色部分)没有任何东西显示它不能向上移动,因此它持续向上移动。在靠近顶部时,它探测到一个障碍物然后改变移动方向。然后它沿着U形障碍物找到它的红色的路径。相反的,一个路径搜索器(pathfinder)将会扫描一个更大的区域(淡蓝色部分),但是它能做到不让物体(unit)走向凹形障碍物而找到一条更短的路径(蓝色路径)。
然而你可以扩展一个运动算法,用于对付上图所示的障碍物。或者避免制造凹形障碍,或者把凹形出口标识为危险的(只有当目的地在里面时才进去):
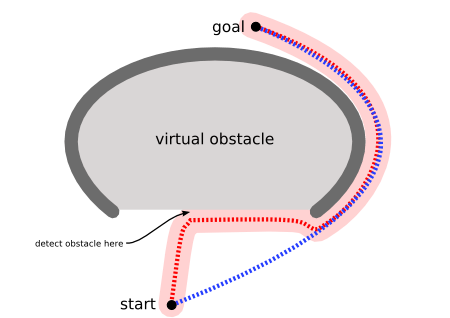
比起一直等到最后一刻才发现问题,路径搜索器让你提前作出计划。不带路径搜索的运动(movement)可以在很多种情形下工作,同时可以扩展到更多的情形,但是路径搜索是一种更常用的解决更多问题的方法。
计算机科学教材中的路径搜索算法在数学视角的图上工作——由边联结起来的结点的集合。一个基于图块(tile)拼接的游戏地图可以看成是一个图,每个图块(tile)是一个结点,并在每个图块之间画一条边:

目前,我会假设我们使用二维网格(grid)。稍后我将讨论如何在你的游戏之外建立其他类型的图。
许多AI领域或算法研究领域中的路径搜索算法是基于任意(arbitrary)的图设计的,而不是基于网格(grid-based)的图。我们可以找到一些能使用网格地图的特性的东西。有一些我们认为是常识,而算法并不理解。例如,我们知道一些和方向有关的东西:一般而言,如果两个物体距离越远,那么把其中一个物体向另一个移动将花越多的时间;并且我们知道地图中没有任何秘密通道可以从一个地点通向另一个地点。(我假设没有,如果有的话,将会很难找到一条好的路径,因为你并不知道要从何处开始。)
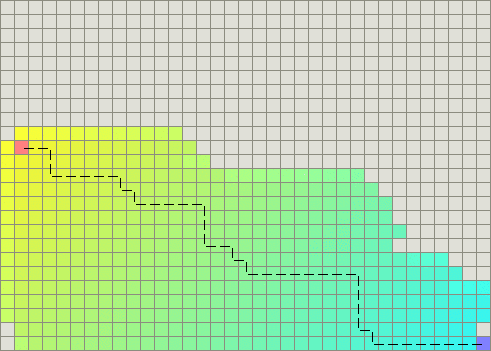
Dijkstra算法从物体所在的初始点开始,访问图中的结点。它迭代检查待检查结点集中的结点,并把和该结点最靠近的尚未检查的结点加入待检查结点集。该结点集从初始结点向外扩展,直到到达目标结点。Dijkstra算法保证能找到一条从初始点到目标点的最短路径,只要所有的边都有一个非负的代价值。(我说“最短路径”是因为经常会出现许多差不多短的路径。)在下图中,粉红色的结点是初始结点,蓝色的是目标点,而类菱形的有色区域(注:原文是teal areas)则是Dijkstra算法扫描过的区域。颜色最淡的区域是那些离初始点最远的,因而形成探测过程(exploration)的边境(frontier):

最佳优先搜索(BFS)算法按照类似的流程运行,不同的是它能够评估(称为启发式的)任意结点到目标点的代价。与选择离初始结点最近的结点不同的是,它选择离目标最近的结点。BFS不能保证找到一条最短路径。然而,它比Dijkstra算法快的多,因为它用了一个启发式函数(heuristic function)快速地导向目标结点。例如,如果目标位于出发点的南方,BFS将趋向于导向南方的路径。在下面的图中,越黄的结点代表越高的启发式值(移动到目标的代价高),而越黑的结点代表越低的启发式值(移动到目标的代价低)。这表明了与Dijkstra 算法相比,BFS运行得更快。

然而,这两个例子都仅仅是最简单的情况——地图中没有障碍物,最短路径是直线的。现在我们来考虑前边描述的凹型障碍物。Dijkstra算法运行得较慢,但确实能保证找到一条最短路径:

另一方面,BFS运行得较快,但是它找到的路径明显不是一条好的路径:
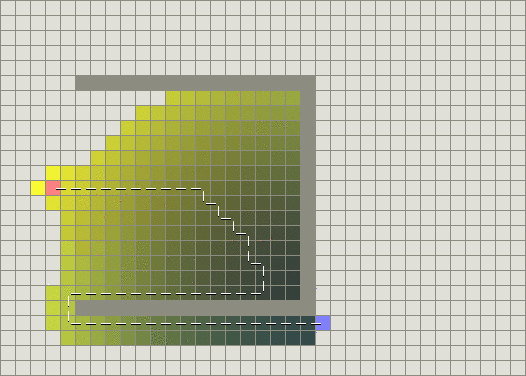
问题在于BFS是基于贪心策略的,它试图向目标移动尽管这不是正确的路径。由于它仅仅考虑到达目标的代价,而忽略了当前已花费的代价,于是尽管路径变得很长,它仍然继续走下去。
结合两者的优点不是更好吗?1968年发明的A*算法就是把启发式方法(heuristic approaches)如BFS,和常规方法如Dijsktra算法结合在一起的算法。有点不同的是,类似BFS的启发式方法经常给出一个近似解而不是保证最佳解。然而,尽管A*基于无法保证最佳解的启发式方法,A*却能保证找到一条最短路径。
我将集中讨论A*算法。A*是路径搜索中最受欢迎的选择,因为它相当灵活,并且能用于多种多样的情形之中。
和其它的图搜索算法一样,A*潜在地搜索图中一个很大的区域。和Dijkstra一样,A*能用于搜索最短路径。和BFS一样,A*能用启发式函数(注:原文为heuristic)引导它自己。在简单的情况中,它和BFS一样快。

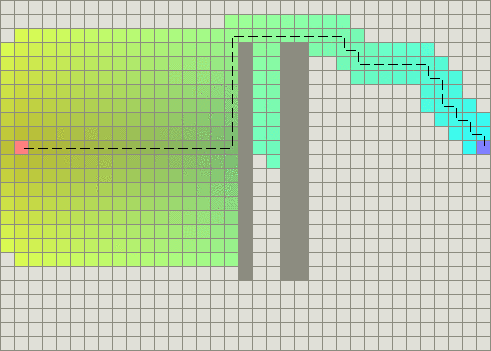
在凹型障碍物的例子中,A*找到一条和Dijkstra算法一样好的路径:
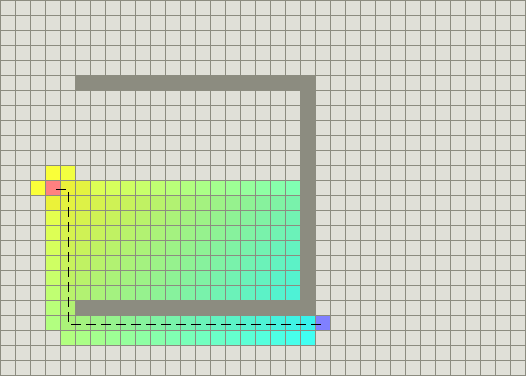
成功的秘决在于,它把Dijkstra算法(靠近初始点的结点)和BFS算法(靠近目标点的结点)的信息块结合起来。在讨论A*的标准术语中,g(n)表示从初始结点到任意结点n的代价,h(n)表示从结点n到目标点的启发式评估代价(heuristic estimated cost)。在上图中,yellow(h)表示远离目标的结点而teal(g)表示远离初始点的结点。当从初始点向目标点移动时,A*权衡这两者。每次进行主循环时,它检查f(n)最小的结点n,其中f(n) = g(n) + h(n)。
启发式函数h(n)告诉A*从任意结点n到目标结点的最小代价评估值。选择一个好的启发式函数是重要的。
启发式函数可以控制A*的行为:
所以我们得到一个很有趣的情况,那就是我们可以决定我们想要从A*中获得什么。理想情况下(注:原文为At exactly the right point),我们想最快地得到最短路径。如果我们的目标太低,我们仍会得到最短路径,不过速度变慢了;如果我们的目标太高,那我们就放弃了最短路径,但A*运行得更快。
在游戏中,A*的这个特性非常有用。例如,你会发现在某些情况下,你希望得到一条好的路径("good" path)而不是一条完美的路径("perfect" path)。为了权衡g(n)和h(n),你可以修改任意一个。
注:在学术上,如果启发式函数值是对实际代价的低估,A*算法被称为简单的A算法(原文为simply A)。然而,我继续称之为A*,因为在实现上是一样的,并且在游戏编程领域并不区别A和A*。
A*改变它自己行为的能力基于启发式代价函数,启发式函数在游戏中非常有用。在速度和精确度之间取得折衷将会让你的游戏运行得更快。在很多游戏中,你并不真正需要得到最好的路径,仅需要近似的就足够了。而你需要什么则取决于游戏中发生着什么,或者运行游戏的机器有多快。
假设你的游戏有两种地形,平原和山地,在平原中的移动代价是1而在山地则是3。A* is going to search three times as far along flat land as it does along mountainous land. 这是因为有可能有一条沿着平原到山地的路径。把两个邻接点之间的评估距离设为1.5可以加速A*的搜索过程。然后A*会将3和1.5比较,这并不比把3和1比较差。It is not as dissatisfied with mountainous terrain, so it won't spend as much time trying to find a way around it. Alternatively, you can speed up up A*'s search by decreasing the amount it searches for paths around mountains―just tell A* that the movement cost on mountains is 2 instead of 3. Now it will search only twice as far along the flat terrain as along mountainous terrain. Either approach gives up ideal paths to get something quicker.
速度和精确度之间的选择前不是静态的。你可以基于CPU的速度、用于路径搜索的时间片数、地图上物体(units)的数量、物体的重要性、组(group)的大小、难度或者其他任何因素来进行动态的选择。取得动态的折衷的一个方法是,建立一个启发式函数用于假定通过一个网格空间的最小代价是1,然后建立一个代价函数(cost function)用于测量(scales):
g’(n) = 1 + alpha * ( g(n) – 1 )
如果alpha是0,则改进后的代价函数的值总是1。这种情况下,地形代价被完全忽略,A*工作变成简单地判断一个网格可否通过。如果alpha是1,则最初的代价函数将起作用,然后你得到了A*的所有优点。你可以设置alpha的值为0到1的任意值。
你也可以考虑对启发式函数的返回值做选择:绝对最小代价或者期望最小代价。例如,如果你的地图大部分地形是代价为2的草地,其它一些地方是代价为1的道路,那么你可以考虑让启发式函数不考虑道路,而只返回2*距离。
速度和精确度之间的选择并不是全局的。在地图上的某些区域,精确度是重要的,你可以基于此进行动态选择。例如,假设我们可能在某点停止重新计算路径或者改变方向,则在接近当前位置的地方,选择一条好的路径则是更重要的,因此为何要对后续路径的精确度感到厌烦?或者,对于在地图上的一个安全区域,最短路径也许并不十分重要,但是当从一个敌人的村庄逃跑时,安全和速度是最重要的。(译者注:译者认为这里指的是,在安全区域,可以考虑不寻找精确的最短路径而取近似路径,因此寻路快;但在危险区域,逃跑的安全性和逃跑速度是重要的,即路径的精确度是重要的,因此可以多花点时间用于寻找精确路径。)
A*计算f(n) = g(n) + h(n)。为了对这两个值进行相加,这两个值必须使用相同的衡量单位。如果g(n)用小时来衡量而h(n)用米来衡量,那么A*将会认为g或者h太大或者太小,因而你将不能得到正确的路径,同时你的A*算法将运行得更慢。
如果你的启发式函数精确地等于实际最佳路径(optimal path),如下一部分的图中所示,你会看到此时A*扩展的结点将非常少。A*算法内部发生的事情是:在每一结点它都计算f(n) = g(n) + h(n)。当h(n)精确地和g(n)匹配(译者注:原文为match)时,f(n)的值在沿着该路径时将不会改变。不在正确路径(right path)上的所有结点的f值均大于正确路径上的f值(译者注:正确路径在这里应该是指最短路径)。如果已经有较低f值的结点,A*将不考虑f值较高的结点,因此它肯定不会偏离最短路径。
构造精确启发函数的一种方法是预先计算任意一对结点之间最短路径的长度。在许多游戏的地图中这并不可行。然后,有几种方法可以近似模拟这种启发函数:
(译者:此处不好翻译,暂时保留原文)
然后添加一个启发函数h’用于评估从任意位置到达邻近导航点(waypoints)的代价。(如果愿意,后者也可以通过预计算得到。)最终的启发式函数可以是:
h(n) = h'(n, w1) + distance(w1, w2), h'(w2, goal)
或者如果你希望一个更好但是更昂贵的启发式函数,则分别用靠近结点和目标的所有的w1,w2对对上式进行求值。(译者注:原文为or if you want a better but more expensive heuristic, evaluate the above with all pairs w1, w2 that are close to the node and the goal, respectively.)
在特殊情况下,你可以不通过预计算而让启发式函数很精确。如果你有一个不存在障碍物和slow地形,那么从初始点到目标的最短路径应该是一条直线。
如果你正使用简单的启发式函数(我们不知道地图上的障碍物),则它应该和精确的启发式函数相符合(译者注:原文为match)。如果不是这样,则你会遇到衡量单位的问题,或者你所选择的启发函数类型的问题。
在网格地图中,有一些众所周知的启发式函数。
标准的启发式函数是曼哈顿距离(Manhattan distance)。考虑你的代价函数并找到从一个位置移动到邻近位置的最小代价D。因此,我的游戏中的启发式函数应该是曼哈顿距离的D倍:
H(n) = D * (abs ( n.x – goal.x ) + abs ( n.y – goal.y ) )
你应该使用符合你的代价函数的衡量单位。

(Note: the above image has a tie-breaker added to the heuristic.}
(译者注:曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离,即D(I,J)=|XI-XJ|+|YI-YJ|。对于一个具有正南正北、正东正西方向规则布局的城镇街道,从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离因此曼哈顿距离又称为出租车距离,曼哈顿距离不是距离不变量,当坐标轴变动时,点间的距离就会不同——百度知道)
如果在你的地图中你允许对角运动那么你需要一个不同的启发函数。(4 east, 4 north)的曼哈顿距离将变成8*D。然而,你可以简单地移动(4 northeast)代替,所以启发函数应该是4*D。这个函数使用对角线,假设直线和对角线的代价都是D:
h(n) = D * max(abs(n.x - goal.x), abs(n.y - goal.y))

如果对角线运动的代价不是D,但类似于D2 = sqrt(2) * D,则上面的启发函数不准确。你需要一些更准确(原文为sophisticated)的东西:
h_diagonal(n) = min(abs(n.x - goal.x), abs(n.y - goal.y))
h_straight(n) = (abs(n.x - goal.x) + abs(n.y - goal.y))
h(n) = D2 * h_diagonal(n) + D * (h_straight(n) - 2*h_diagonal(n)))
这里,我们计算h_diagonal(n):沿着斜线可以移动的步数;h_straight(n):曼哈顿距离;然后合并这两项,让所有的斜线步都乘以D2,剩下的所有直线步(注意这里是曼哈顿距离的步数减去2倍的斜线步数)都乘以D。
如果你的单位可以沿着任意角度移动(而不是网格方向),那么你也许应该使用直线距离:
h(n) = D * sqrt((n.x-goal.x)^2 + (n.y-goal.y)^2)
然而,如果是这样的话,直接使用A*时将会遇到麻烦,因为代价函数g不会match启发函数h。因为欧几里得距离比曼哈顿距离和对角线距离都短,你仍可以得到最短路径,不过A*将运行得更久一些:
我曾经看到一些A*的网页,其中提到让你通过使用距离的平方而避免欧几里得距离中昂贵的平方根运算:
h(n) = D * ((n.x-goal.x)^2 + (n.y-goal.y)^2)
不要这样做!这明显地导致衡量单位的问题。当A*计算f(n) = g(n) + h(n),距离的平方将比g的代价大很多,并且你会因为启发式函数评估值过高而停止。对于更长的距离,这样做会靠近g(n)的极端情况而不再计算任何东西,A*退化成BFS:

导致低性能的一个原因来自于启发函数的ties(注:这个词实在不知道应该翻译为什么)。当某些路径具有相同的f值的时候,它们都会被搜索(explored),尽管我们只需要搜索其中的一条:
Ties in f values.
为了解决这个问题,我们可以为启发函数添加一个附加值(译者注:原文为small tie breaker)。附加值对于结点必须是确定性的(也就是说,不能是随机的数),而且它必须让f值体现区别。因为A*对f值排序,让f值不同意味着只有一个"equivalent"的f值会被检测。
一种添加附加值的方式是稍微改变(译者注:原文为nudge)h的衡量单位。如果我们减少衡量单位(译者注:原文为scale it downwards),那么当我们朝着目标移动的时候f将逐渐增加。很不幸,这意味着A*倾向于扩展到靠近初始点的结点,而不是靠近目标的结点。我们可以增加衡量单位(译者注:原文为scale it downwards scale h upwards slightly)(甚至是0.1%),A*就会倾向于扩展到靠近目标的结点。
heuristic *= (1.0 + p)
选择因子p使得p < 移动一步(step)的最小代价 / 期望的最长路径长度。假设你不希望你的路径超过1000步(step),你可以使p = 1 / 1000。添加这个附加值的结果是,A*比以前搜索的结点更少了。

Tie-breaking scaling added to heuristic.
当存在障碍物时,当然仍要在它们周围寻找路径,但要意识到,当绕过障碍物以后,A*搜索的区域非常少:
Tie-breaking scaling added to heuristic, works nicely with obstacles.
Steven van Dijk建议,一个更直截了当的方法是把h传递到比较函数(comparison function)。当f值相等时,比较函数检查h,然后添加附加值。
一个不同的添加附加值的方法是,倾向于从初始点到目标点的连线(直线):
dx1 = current.x - goal.x
dy1 = current.y - goal.y
dx2 = start.x - goal.x
dy2 = start.y - goal.y
cross = abs(dx1*dy2 - dx2*dy1)
heuristic += cross*0.001
这段代码计算初始-目标向量(start to goal vector)和当前-目标向量(current point to goal vector)的向量叉积(vector cross-product)。When these vectors don't line up, the cross product will be larger.结果是,这段代码选择的路径稍微倾向于从初始点到目标点的直线。当没有障碍物时,A*不仅搜索很少的区域,而且它找到的路径看起来非常棒:

Tie-breaking cross-product added to heuristic, produces pretty paths.
然而,因为这种附加值倾向于从初始点到目标点的直线路径,当出现障碍物时将会出现奇怪的结果(注意这条路径仍是最佳的,只是看起来很奇怪):

Tie-breaking cross-product added to heuristic, less pretty with obstacles.
为了交互地研究这种附加值方法的改进,请参考James Macgill的A*确applet(http://www.ccg.leeds.ac.uk/james/aStar/ )[如果链接无效,请使用这个镜像(http://www.vision.ee.ethz.ch/~buc/astar/AStar.html)](译者注:两个链接均无效)。使用“Clear”以清除地图,选择地图对角的两个点。当你使用“Classic A*”方法,你会看到附加值的效果。当你使用“Fudge”方法,你会看到上面给启发函数添加叉积后的效果。
然而另一种添加附加值的方法是,小心地构造你的A*优先队列,使新插入的具有特殊f值的结点总是比那些以前插入的具有相同f值的旧结点要好一些。
你也许也想看看能够更灵活地(译者注:原文为sophisticated)添加附加值的AlphA*算法(http://home1.stofanet.dk/breese/papers.html),不过用这种算法得到的路径是否能达到最佳仍在研究中。AlphA*具有较好的适应性,而且可能比我在上面讨论的附加值方法运行得都要好。然而,我所讨论的附加值方法非常容易实现,所以从它们开始吧,如果你需要得到更好的效果,再去尝试AlphA*。
如果你想搜索邻近目标的任意不确定结点,而不是某个特定的结点,你应该建立一个启发函数h’(x),使得h’(x)为h1(x), h2(x), h3(x)。。。的最小值,而这些h1, h2, h3是邻近结点的启发函数。然而,一种更快的方法是让A*仅搜索目标区域的中心。一旦你从OPEN集合中取得任意一个邻近目标的结点,你就可以停止搜索并建立一条路径了。
如果不考虑具体实现代码,A*算法是相当简单的。有两个集合,OPEN集和CLOSED集。其中OPEN集保存待考查的结点。开始时,OPEN集只包含一个元素:初始结点。CLOSED集保存已考查过的结点。开始时,CLOSED集是空的。如果绘成图,OPEN集就是被访问区域的边境(frontier)而CLOSED集则是被访问区域的内部(interior)。每个结点同时保存其父结点的指针因此我们可以知道它是如何被找到的。
在主循环中重复地从OPEN集中取出最好的结点n(f值最小的结点)并检查之。如果n是目标结点,则我们的任务完成了。否则,结点n被从OPEN集中删除并加入CLOSED集。然后检查它的邻居n’。如果邻居n’在CLOSED集中,那么它是已经被检查过的,所以我们不需要考虑它*;如果n’在OPEN集中,那么它是以后肯定会被检查的,所以我们现在不考虑它*。否则,把它加入OPEN集,把它的父结点设为n。到达n’的路径的代价g(n’),设定为g(n) + movementcost(n, n’)。
(*)这里我忽略了一个小细节。你确实需要检查结点的g值是否更小了,如果是的话,需要重新打开(re-open)它。
OPEN = priority queue containing START
CLOSED = empty set
while lowest rank in OPEN is not the GOAL:
current = remove lowest rank item from OPEN
add current to CLOSED
for neighbors of current:
cost = g(current) + movementcost(current, neighbor)
if neighbor in OPEN and cost less than g(neighbor):
remove neighbor from OPEN, because new path is better
if neighbor in CLOSED and cost less than g(neighbor): **
remove neighbor from CLOSED
if neighbor not in OPEN and neighbor not in CLOSED:
set g(neighbor) to cost
add neighbor to OPEN
set priority queue rank to g(neighbor) + h(neighbor)
set neighbor's parent to current
reconstruct reverse path from goal to start
by following parent pointers
(**) This should never happen if you have an admissible heuristic. However in games we often have inadmissible heuristics.
我自己的(旧的)C++A*代码是可用的:path.cpp (http://theory.stanford.edu/~amitp/ GameProgramming/path.cpp)和path.h (http://theory.stanford.edu/~amitp/GameProgramming/ path.h),但是不容易阅读。还有一份更老的代码(更慢的,但是更容易理解),和很多其它的A*实现一样,它在Steve Woodcock'的游戏AI页面(http://www.gameai.com/ai.html)。
在网上,你能找到C,C++,Visual Basic ,Java(http://www.cuspy.com/software/pathfinder/ doc/),Flash/Director/Lingo, C#(http://www.codeproject.com/csharp/CSharpPathfind.asp), Delphi, Lisp, Python, Perl, 和Prolog 实现的A*代码。一定的阅读Justin Heyes-Jones的C++实现(http://www.geocities.com/jheyesjones/astar.html)。
你首先想到的用于实现OPEN集和CLOSED集的数据结构是什么?如果你和我一样,你可能想到“数组”。你也可能想到“链表”。我们可以使用很多种不同的数据结构,为了选择一种,我们应该考虑我们需要什么样的操作。
在OPEN集上我们主要有三种操作:主循环重复选择最好的结点并删除它;访问邻居结点时需要检查它是否在集合里面;访问邻居结点时需要插入新结点。插入和删除最佳是优先队列(http://members.xoom.com/killough/heaps.html)的典型操作。
选择哪种数据结构不仅取决于操作,还取决于每种操作执行的次数。检查一个结点是否在集合中这一操作对每个被访问的结点的每个邻居结点都执行一次。删除最佳操作对每个被访问的结点都执行一次。被考虑到的绝大多数结点都会被访问;不被访问的是搜索空间边缘(fringe)的结点。当评估数据结构上面的这些操作时,必须考虑fringe(F)的最大值。
另外,还有第四种操作,虽然执行的次数相对很少,但还是必须实现的。如果正被检查的结点已经在OPEN集中(这经常发生),并且如果它的f值比已经在OPEN集中的结点要好(这很少见),那么OPEN集中的值必须被调整。调整操作包括删除结点(f值不是最佳的结点)和重插入。这两个步骤必须被最优化为一个步骤,这个步骤将移动结点。
最简单的数据结构是未排序数组或链表。集合关系检查操作(Membership test)很慢,扫描整个结构花费O(F)。插入操作很快,添加到末尾花费O(1)。查找最佳元素(Finding the best element)很慢,扫描整个结构花费O(F)。对于数组,删除最佳元素(Removing the best element)花费O(F),而链表则是O(1)。调整操作中,查找结点花费O(F),改变值花费O(1)。
为了加快删除最挂操作,可以对数组进行排序。集合关系检查操作将变成O(log F),因为我们可以使用折半查找。插入操作会很慢,为了给新元素腾出空间,需要花费 O(F)以移动所有的元素。查找最佳元素操作会很快,因为它已经在末尾了所以花费是O(1)。如果我们保证最佳排序至数组的尾部(best sorts to the end of the array),删除最佳元素操作花费将是O(1)。调整操作中,查找结点花费O(logF),改变值/位置花费O(F)。
在排序数组中,插入操作很慢。如果使用链表则可以加速该操作。集合关系检查操作很慢,需要花费O(F)用于扫描链表。插入操作是很快的,插入新元素只花费O(1)时间,但是查找正确位置需要花费O(F)。查找最佳元素很快,花费O(1)时间,因为最佳元素已经在表的尾部。删除最佳元素也是O(1)。调整操作中,查找结点花费O(F),改变值/位置花费O(1)。
在未排序链表中查找元素是很慢的。如果用跳表(http://en.wikipedia.org/wiki/Skip_list)代替链表的话,可以加速这个操作。在跳表中,如果有排序键(sort key)的话,集合关系检查操作会很快:O(log F)。如果你知道在何处插入的话,和链表一样,插入操作也是O(1)。如果排序键是f,查找最佳元素很快,达到O(1),删除一个元素也是O(1)。调整操作涉及到查找结点,删除结点和重插入。
如果我们用地图位置作为跳表的排序键,集合关系检查操作将是O(log F)。在完成集合关系检查后,插入操作是O(1)。查找最佳元素是O(F),删除一个结点是O(1)。因为集合关系检查更快,所以它比未排序链表要好一些。
如果我们用f值作为跳表的排序键,集合关系检查操作将是O(F)。插入操作是O(1)。查找最佳元素是O(1),删除一个结点是O(1)。这并不比排序链表好。
如果结点的集合有限并且数目是适当的,我们可以使用直接索引结构,索引函数i(n)把结点n映射到一个数组的索引。未排序与排序数组的长度等于OPEN集的最大值,和它们不同,对所有的n,索引数组的长度总是等于max(i(n))。如果你的函数是密集的(没有不被使用的索引),max(i(n))将是你地图中结点的数目。只要你的地图是网格的,让索引函数密集就是容易的。
假设i(n)是O(1)的,集合关系检查将花费O(1),因为我们几乎不需要检查Array[i(n)]是否包含任何数据。Insertion is O(1), as we just ste Array[i(n)].查找和删除最佳操作是O(numnodes),因为我们必须搜索整个结构。调整操作是O(1)。
索引数组使用了很多内存用于保存不在OPEN集中的所有结点。一个选择是使用哈希表。哈希表使用了一个哈希函数h(n)把地图上每个结点映射到一个哈希码。让哈希表的大小等于N的两倍,以使发生冲突的可能性降低。假设h(n) 是O(1)的,集体关系检查操作花费O(1);插入操作花费O(1);删除最佳元素操作花费O(numnodes),因为我们需要搜索整个结构。调整操作花费O(1)。
一个二元堆(不要和内存堆混淆)是一种保存在数组中的树结构。和许多普通的树通过指针指向子结点所不同,二元堆使用索引来查找子结点。C++ STL包含了一个二元堆的高效实现,我在我自己的A*代码中使用了它。
在二元堆中,集体关系检查花费O(F),因为你必须扫描整个结构。插入操作花费O(log F)而删除最佳操作花费也是O(log F)。调整操作很微妙(tricky),花费O(F)时间找到节点,并且很神奇,只用O(log F)来调整。
我的一个朋友(他研究用于最短路径算法的数据结构)说,除非在你的fringe集里有多于10000个元素,否则二元堆是很不错的。除非你的游戏地图特别大,否则你不需要更复杂的数据结构(如multi-level buckets(http://www-cs-students.stanford.edu/~csilvers/))。你应该尽可能不用Fibonacci 堆(http://www.star-lab.com/goldberg/pub/neci-tr-96-062.ps),因为虽然它的渐近复杂度很好,但是执行起来很慢,除非F足够大。
堆是一种基于树的结构,它有一个期望的O(log F)代价的时间操作。然而,问题是在A*算法中,通常的情况是,一个代价小的节点被移除(花费O(log F)的代价,因为其他结点必须从树的底部向上移动),而紧接着一些代价小的节点被添加(花费O(log F)的代价,因为这些结点被添加到底部并且被移动到最顶部)。在这里,堆的操作在预期的情况下和最坏情况下是一样的。如果我们找到这样一种数据结构,最坏情况还是一样,而预期的情况好一些,那么就可以得到改进。
伸展树(Splay tree)是一种自调整的树结构。任何对树结点的访问都尝试把该结点推到树的顶部(top)。这就产生了一个缓存效果("caching" effect):很少被使用的结点跑到底部(bottom)去了并且不减慢操作(don't slow down operations)。你的splay树有多大并不重要,因为你的操作仅仅和你的“cache size”一样慢。在A*中,低代价的结点使用得很多,而高代价结点经常不被使用,所以高代价结点将会移动到树的底部。
使用伸展树后,集体关系检查,插入,删除最佳和调整操作都是期望的O(log F)(注:原文为expected O(log F) ),最坏情况是O(F)。然而有代表性的是,缓存过程(caching)避免了最坏情况的发生。Dijkstra算法和带有低估的启发函数(underestimating heuristic)的A*算法却有一些特性让伸展树达不到最优。特别是对结点n和邻居结点n’来说,f(n') >= f(n)。当这发生时,也许插入操作总是发生在树的同一边结果是使它失去了平衡。我没有试验过这个。
还有一种比堆好的数据结构。通常你可以限制优先队列中值的范围。给定一个限定的范围,经常会存在更好的算法。例如,对任意值的排序可以在O(N log N)时间内完成,但当固定范围时,桶排序和基数排序可以在O(N)时间内完成。
我们可以使用HOT(Heap On Top)队列(http://www.star-lab.com/goldberg/pub /neci-tr-97-104.ps)来利用f(n') >= f(n),其中n’是n的一个邻居结点。我们删除f(n)值最小的结点n,插入满足f(n) <= f(n') <= f(n) + delta的邻居n',其中delta <= C。常数C是从一结点到邻近结点代价改变量的最大值。因为f(n)是OPEN集中的最小f值,并且正要被插入的所有结点都小于或等于f(n) + delta,我们知道OPEN集中的所有f值都不超过一个0..delta的范围。在桶/基数排序中,我们可以用“桶”(buckets)对OPEN集中的结点进行排序。
使用K个桶,我们把O(N)的代价降低到平均O(N/K)。通过HOT队列,顶端的桶使用二元堆而所有其他的桶都是未排序数组。因而,对顶部的桶,集合关系检查代价是预期的O(F/K),插入和删除最佳是O(log (F/K))。对其他桶,集合关系检查是O(F/K),插入是O(1),而删除最佳根本不发生!如果顶端的桶是空的,那么我们必须把下一个桶即未排序数组转换为二元堆。这个操作(“heapify”)可以在O(F/K)时间内完成。在调整操作中,删除是O(F/K),然后插入是O(log (F/K))或O(1)。
在A*中,我们加入OPEN集中的许多结点实际上根本是不需要的。在这方面HOT队列很有优势,因为不需要的元素的插入操作只花费O(1)时间。只有需要的元素被heapified(代价较低的那些)。唯一一个超过O(1)的操作是从堆中删除结点,只花费O(log (F/K))。
另外,如果C比较小,我们可以只让K = C,则对于最小的桶,我们甚至不需要一个堆,国为在一个桶中的所有结点都有相同的f值。插入和删除最佳都是O(1)时间!有人研究过,HOT队列在至多在OPEN集中有800个结点时和堆一样快,并且如果OPEN集中至多有1500个结点,则比堆快20%。我期望随着结点的增加,HOT队列也更快。
HOT队列的一个简单的变化是一个二层队列(two-level queue):把好的结点放进一个数据结构(堆或数组)而把坏的结点放进另一个数据结构(数组或链表)。因为大多数进入OPEN集中的结点都“坏的”,它们从不被检查,因而把它们放进出一个大数组是没有害处的。
注意有一点很重要,我们并不是仅仅关心渐近的行为(大O符号)。我们也需要关心小常数(low constant)下的行为。为了说明原因,考虑一个O(log F)的算法,和另一个O(F)的算法,其中F是堆中元素的个数。也许在你的机器上,第一个算法的实现花费10000*log(F)秒,而另一个的实现花费2*F秒。当F=256时,第一个算法将花费80000秒而第二个算法花费512秒。在这种情况下,“更快”的算法花费更多的时间,而且只有在当F>200000时才能运行得更快。
你不能仅仅比较两个算法。你还要比较算法的实现。同时你还需要知道你的数据的大小(size)。在上面的例子中,第一种实现在F>200000时更快,但如果在你的游戏中,F小于30000,那么第二种实现好一些。
基本数据结构没有一种是完全合适的。未排序数组或者链表使插入操作很快而集体关系检查和删除操作非常慢。排序数组或者链表使集体关系检查稍微快一些,删除(最佳元素)操作非常快而插入操作非常慢。二元堆让插入和删除操作稍微快一些,而集体关系检查则很慢。伸展树让所有操作都快一些。HOT队列让插入操作很快,删除操作相当快,而集体关系检查操作稍微快一些。索引数组让集体关系检查和插入操作非常快,但是删除操作不可置信地慢,同时还需要花费很多内存空间。哈希表和索引数组类似,但在普通情况下,它花费的内存空间少得多,而删除操作虽然还是很慢,但比索引数组要快。
关于更高级的优先队列的资料和实现,请参考Lee Killough的优先队列页面(http://members.xoom.com/killough/heaps.html)。
为了得到最佳性能,你将希望使用混合数据结构。在我的A*代码中,我使用一个索引数组从而集合关系检查是O(1)的,一个二元堆从而插入操作和删除最佳都是O(log F)的。对于调整操作,我使用索引数组从而花费O(1)时间检查我是否真的需要进行调整(通过在索引数组中保存g值),然后在少数确实需要进行调整的情况中,我使用二元堆从而调整操作花费O(F)时间。你也可以使用索引数组保存堆中每个结点的位置,这让你的调整操作变成O(log F)。
交互式的(尤其是实时的)游戏对最佳路径的计算要求很高。能够得到一个解决方案比得到最佳方案可能更重要。然而在所有其他因素都相同的情况下,短路径比长路径好。
一般来说,计算靠近初始结点的路径比靠近目标结点的路径更重要一些。立即开始原理(The principle of immediate start):让游戏中的物体尽可能快地开始行动,哪怕是沿着一条不理想的路径,然后再计算一条更好的路径。在实时游戏中,应该更多地关注A*的延迟情况(latency)而不是吞吐量(throughput)。
可以对物体编程让它们根据自己的本能(简单行为)或者智力(一条预先计算好的路径)来行动。除非它们的智力告诉它们怎么行动,否则它们就根据自己的本能来行动(这是实际上使用的方法,并且Rodney Brook在他的机器人体系结构中也用到)。和立即计算所有路径所不同,让游戏在每一个,两个,或者三个循环中搜索一条路径。让物体在开始时依照本能行动(可能仅仅是简单地朝着目标直线前进),然后才为它们寻找路径。这种方法让让路径搜索的代价趋于平缓,因此它不会集中发生在同一时刻。
可以从A*算法的主循环中提前退出来同时得到一条局部路径。通常,当找到目标结点时,主循环就退出了。然而,在此之前的任意结点,可以得到一条到达OPEN中当前最佳结点的路径。这个结点是到达目标点的最佳选择,所以它是一个理想的
如果觉得我的文章对您有用,请随意打赏。你的支持将鼓励我继续创作!
