社区微信群开通啦,扫一扫抢先加入社区官方微信群

社区微信群
社区微信群开通啦,扫一扫抢先加入社区官方微信群

社区微信群
以上三个算法的基本概念,网上有更多资料,这里就不详细展开了。接下来讲我在学习过程中遭遇的问题。在实际运用这些算法解题的时候,经常会看到一些很奇怪的名词,比如解空间、自顶向下解法、自底向上解法等等。那么这些词到底代表的是什么含义呢?接下来通过一些具体的例子和图来展示。
问题描述
斐波那契数列是通过"递归"定义的,通过这个递归关系式,我们可以知道斐波那契数列中任意一个位置的数值。给你一个数字n,你能求出它对应的数列值是多少嘛?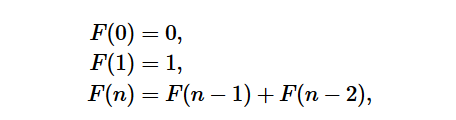
回溯法
如果要求F(n),那么必须要知道F(n-1)和F(n-2)。其问题就变成了求F(n-1)和F(n-2)。
举个例子,当我们计算f(7)的时候,必须要知道f(5)和f(6),而计算f(5)又必须要知道f(3)和f(4),直到问题规模缩小至f(0)和f(1)的时候,我们才能够根据已有的条件得到答案,然后往上回推。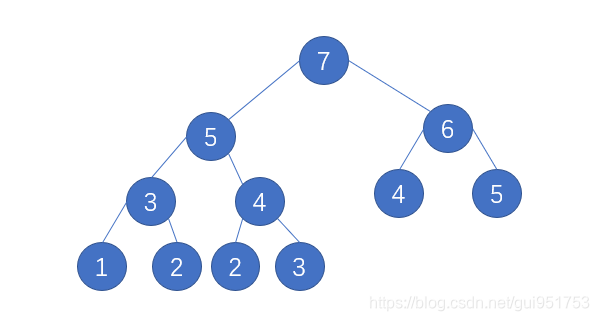
代码示意如下
def f(n):
if n==0:
return 0
if n==1:
return 1
return f(n-1)+f(n-2)
动态规划
使用回溯法解题的时候,习惯于把大问题分解,分解到问题规模可解的时候,再去解决问题。而动态规划则是从已知解出发,逐步推算到问题规模的程度。
对于斐波那契数列问题而言,还拿f(7)举例,其过程如下:
通过分析这个过程可以知道,动态规划的出发点是叶子节点,通过公式,逐步的从叶子结点上推到根节点。其核心思想就是通过已知解,来求解未知解。直到求解到的问题规模符合题目要求的规模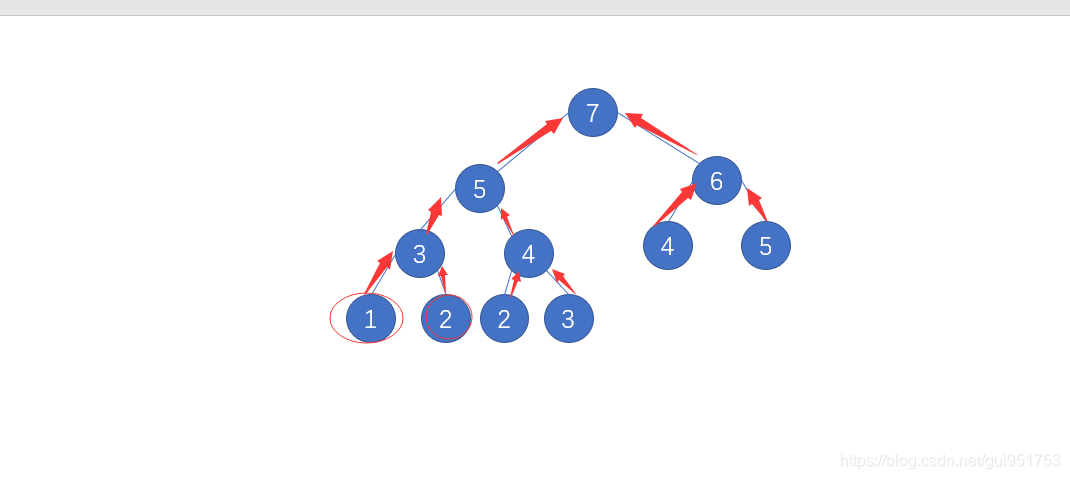 代码实现如下:
代码实现如下:
def f(n):
#定义一个长度为n+1的数组,用来存储和记录已经计算过的值
a=[0]*(n+1)
# 初始化已知解
a[0]=0,a[1]=1
# 利用公式进行递推,不断推导未知解,直到求出自己想要的未知解,停止。
for i in range(2,n+1):
a[i]=a[i-1]+a[i-2]
return a[n]
总结
上文主要描述了解题的时候,回溯法和动态规划之间的区别。主要有以下几点。
问题描述: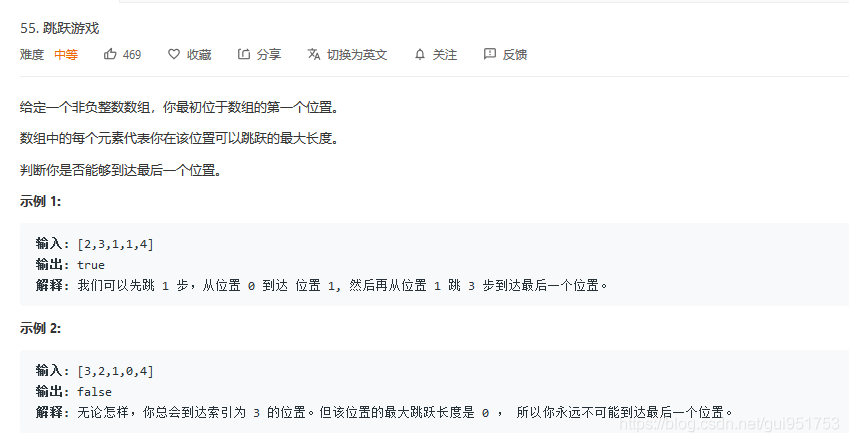
这道题目是leetcode的原题,其官方解答对理解动态规划和回溯的优异和异同具有很大的帮助。官方解答过程:回溯法——》带记忆表的回溯法———》动态规划——》贪心。
回溯法
首先,通过题目可以知道这是一个多阶段问题。拿例子[2,3,1,1,4]为例。位置0的值为2,因此可以跳到位置1和位置2。到底跳到位置几,需要我们自己判断。如果判断不出来,那么最简单的思路就是枚举。把所有情况都枚举一遍。我用了一幅图来表示枚举的过程。
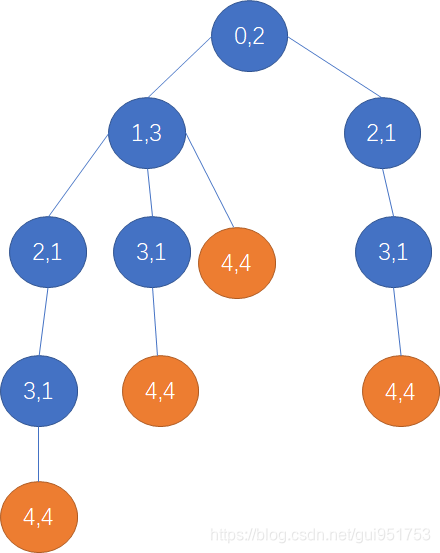
# 我用伪代码描述下这个过程。
# 给定一个数组a和它开始跳的时候的下标。
def can_jump_from_position(pos,a):
#如果到达叶子节点(已知解),那么一定可以到达。
if pos == len(a):
return True
#对当前节点进行扩展,推导它的子节点。
furthest_jump = min(a[pos]+pos,len(a)-1) #当前节点最远能跳的距离受制于数组下标的最大值。不能超过数组下标。
#扩展子节点
for next_pos in range(pos+1,furthest_jump+1):
# 子节点有解,则父节点也一定有解,故返回True
if can_jump_from_postion(next_pos,a):
return True
#所有子节点都无解,返回False
return False
#调用该回溯算法
def can_jump(a):
return can_jump_from_postion(0,a)
回溯法总结
对于一个问题,如果用回溯法解题,可以抽象出这样的思路。
回溯优化
对于整个回溯过程,普遍存在的问题是会存在着大量计算。比较好的优化思路是使用一个数组去记录已经得到的解。这样下次查询的时候,先判断一下是否已经解过了就好了。这个思路,leetcode有相应的说明。可以看题解。其中初始化最后一个坐标为GOOD的原因是它就是我们已经知道的已知解。
动态规划
对于动态规划来说,其核心思想就是通过已知解求解未知解。对当前这个题目来说,已知解就是最后一个坐标是能够到达最后一个坐标的。最后一个坐标就是叶子节点,问题是能否从坐标0到达最后一个节点,坐标0就是根节点。整个从叶子结点(已知解)到根节点(未知问题)的分析过程,就是自下而上的分析过程。
拿[2,3,1,1,4]这个例子来说,已知位置4是能够到达最后一个坐标的,是已知解,是叶子结点。接下来只需要判断其叶子节点的上一层能否有解即可缩小问题规模。比如说位置3是可以到达位置4的,那么整个问题就从“是否能从位置0到最后一个位置(位置4)”变为“是否能从位置0到达位置3”。因为位置3是可以到达位置4的。
其过程如下:
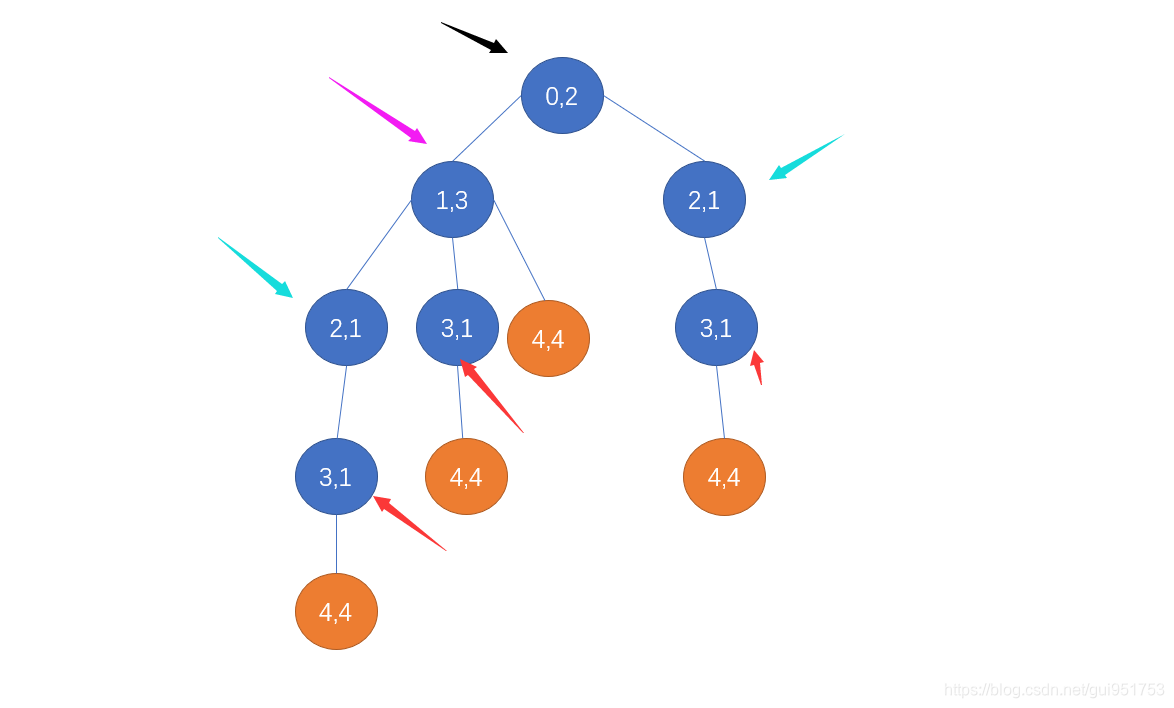
代码思路展示
#需要从已知解出发,扩展出未知解。
def can_jump(a):
#使用一个数组记录解的情况
a_len = len(a)
dp = [0]*a_len
#初始化已知解,最后一个坐标一定可达
dp[a_len-1] = 1
#从叶子节点往上倒推,并把有解的记录下来。
for i in range(a_len-2,-1,-1):
furthest_jump = min(a[i]+i,a_len-1)
#遍历当前节点的所有子节点
for j in range(i,furthest_jump+1):
#如果子节点有解,那么当前节点一定有解
if dp[j] == 1:
dp[i] == 1
return dp[0] == 1
贪心算法
对于这个问题,还有一种解法,就是贪心算法。如果一个问题能使用贪心解决,那么需要它的每个子问题的最优解都是全局最优解的一部分。其实,我感觉判断是否可以用贪心,多半靠经验,如果刷题的话,不太好证明到底能不能用贪心,只能举反例。
还是这个解空间,其贪心过程如下。
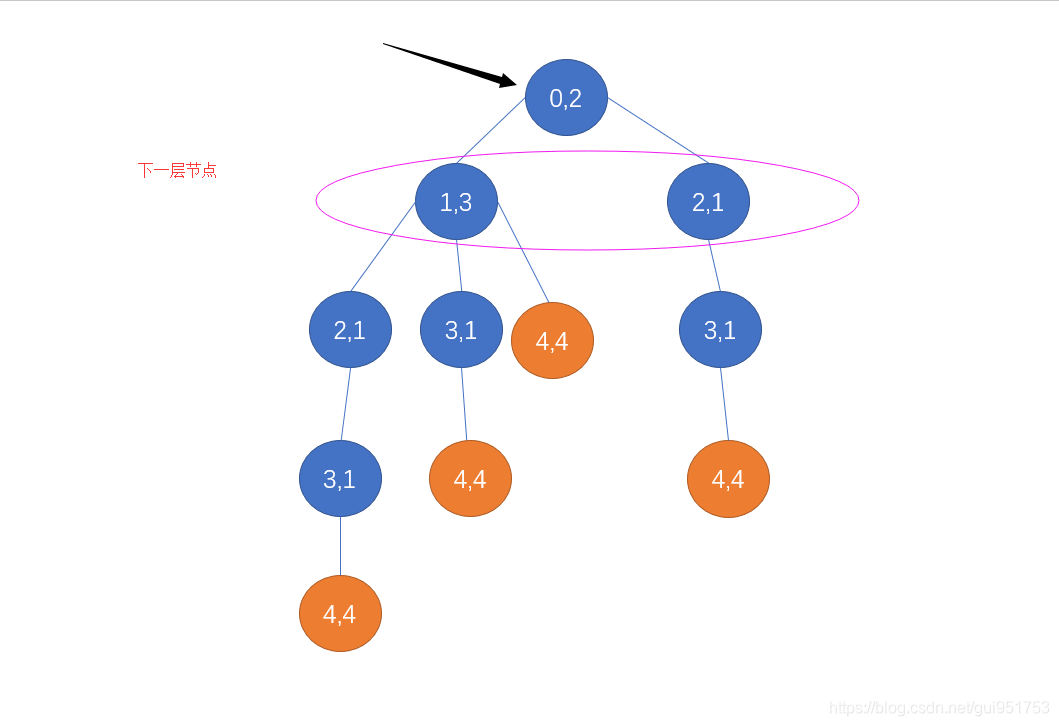
def can_jump(a):
# end 记录下层能跳的边界
# max_pos记录下层能跳的最大距离
# step 记录跳数
end = max_pos = 0
for i in range(0,len(a)):
# 出现0的时候max_pos有可能会停滞,如果停滞了,那就代表无法继续了
if i < max_pos:
return False
max_pos = max(a[i]+i,max_pos)
#当前层已走完,记录下一层的边界
if end == i :
step += 1
end = max_pos
return max_pos > len(a)-1
这种方法也可以记录跳数。
以上代码都是白板乱写的,不一定能运行,大家看个思路就好。
本篇文章主要讲了DP和回溯法解题的区别。我觉得最主要的有以下几点。
其实我觉得能看懂自顶向下和自底向上的分析过程就是最大的收获了
如果觉得我的文章对您有用,请随意打赏。你的支持将鼓励我继续创作!
